Time Series Analysis in Python for Data Analyics
Table of Contents
ToggleWhat is a Time Series?

A time series is a set of data points collected or recorded at regular intervals. These data points can represent any measurable quantity or occurrence that changes over time, including stock prices, temperature readings, sales figures, and sensor data. Time series data is widely used in industries such as finance, economics, weather forecasting, signal processing, and engineering.
Key characteristics of time series data include:
- Temporal Ordering: Data points are sorted in chronological order, with each observation assigned a precise time index or timestamp.
- Equally Spaced Intervals: Time intervals between consecutive data values are normally uniform, but irregular intervals may exist in rare instances.
- Sequential reliance: There is frequently some type of reliance or relationship between consecutive observations in a time series, such as trends, seasonality, autocorrelation, or other patterns.
Understanding and modeling temporal dependencies is required for analyzing time series data in order to find core patterns, create forecasts, spot problems, or do other sorts of analysis unique to the application area.
Why even analyze a time series?
Because it is the first stage in developing a series forecast.
Furthermore, time series forecasting has huge commercial significance because vital business metrics like as demand and sales, number of visitors to a website, stock price, and so on are fundamentally time series data.
So what does analyzing a time series involve?
Time series analysis entails knowing numerous factors regarding the underlying nature of the series in order to develop meaningful and reliable projections.
How to import time series in python?
The date and the measured value are the two columns that make up the data for a time series, which is usually stored in.csv files or other spreadsheet formats.
To read the time series dataset as a pandas dataframe, let’s utilize the read_csv() function in the pandas package. The date column can be parsed as a date field by adding the parse_dates=[‘date’] option.
from dateutil.parser import parse
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd
plt.rcParams.update({'figure.figsize': (10, 7), 'figure.dpi': 120})
# Import as Dataframe
df = pd.read_csv(r'C:\Users\VIVEK\Downloads/a10.csv', parse_dates=['date'])
df.head()
Alternately, you can import it as a pandas Series with the date as index. You just need to specify the index_col argument in the pd.read_csv() to do this.
ser = pd.read_csv(r'C:\Users\VIVEK\Downloads/a10.csv', parse_dates=['date'], index_col='date')
ser.head()
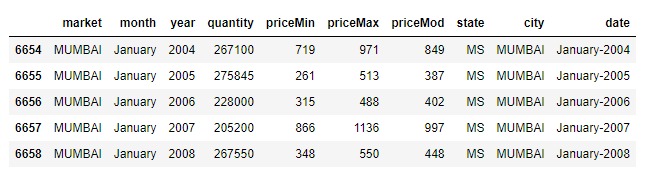
What is panel data?
Another time-based dataset is panel data.
The distinction is that it includes one or more related variables that are measured for the same time periods in addition to the time series.
If the explanatory variables in the panel data are still accessible for the upcoming forecasting period, they usually include columns that can be useful in projecting the Y.
Below is an example of panel data.
df = pd.read_csv(r'C:\Users\VIVEK\Downloads/MarketArrivals.csv')
df = df.loc[df.market=='MUMBAI', :]
df.head()
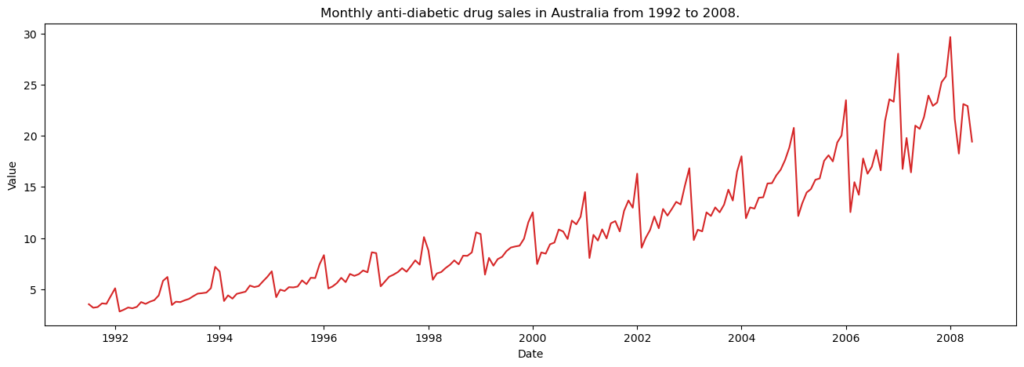
Visualizing a time series
Let’s use matplotlib to visualise the series.
import matplotlib.pyplot as plt
import pandas as pd
df = pd.read_csv(r'C:\Users\VIVEK\Downloads/a10.csv', parse_dates=['date'], index_col='date')
# Draw Plot
def plot_df(df, x, y, title="", xlabel='Date', ylabel='Value', dpi=100):
plt.figure(figsize=(16,5), dpi=dpi)
plt.plot(x, y, color='tab:red')
plt.gca().set(title=title, xlabel=xlabel, ylabel=ylabel)
plt.show()
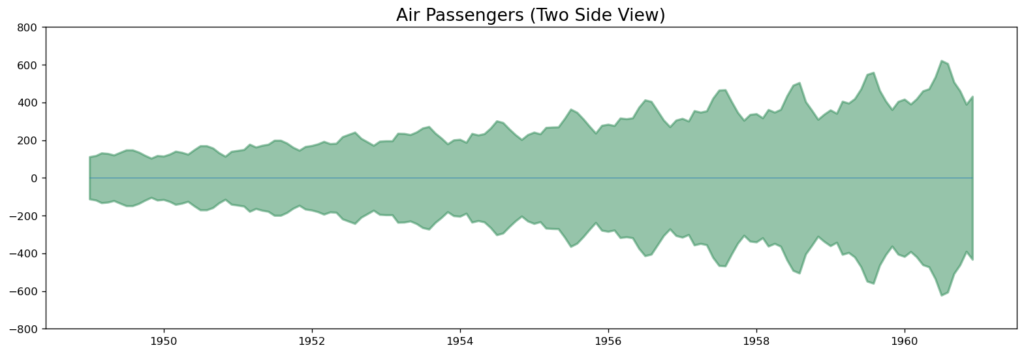
plot_df(df, x=df.index, y=df.value, title='Monthly anti-diabetic drug sales in Australia from 1992 to 2008.')
Since all values are positive, you can show this on both sides of the Y axis to emphasize the growth.
# Import data
import pandas as pd
df = pd.read_csv(r'C:\Users\VIVEK\Downloads/AirPassengers.csv', parse_dates=['Month'])
x = df['Month'].values
y1 = df['#Passengers'].values
# Plot
fig, ax = plt.subplots(1, 1, figsize=(16,5), dpi= 120)
plt.fill_between(x, y1=y1, y2=-y1, alpha=0.5, linewidth=2, color='seagreen')
plt.ylim(-800, 800)
plt.title('Air Passengers (Two Side View)', fontsize=16)
plt.hlines(y=0, xmin=np.min(df.Month), xmax=np.max(df.Month), linewidth=.5)
plt.show()
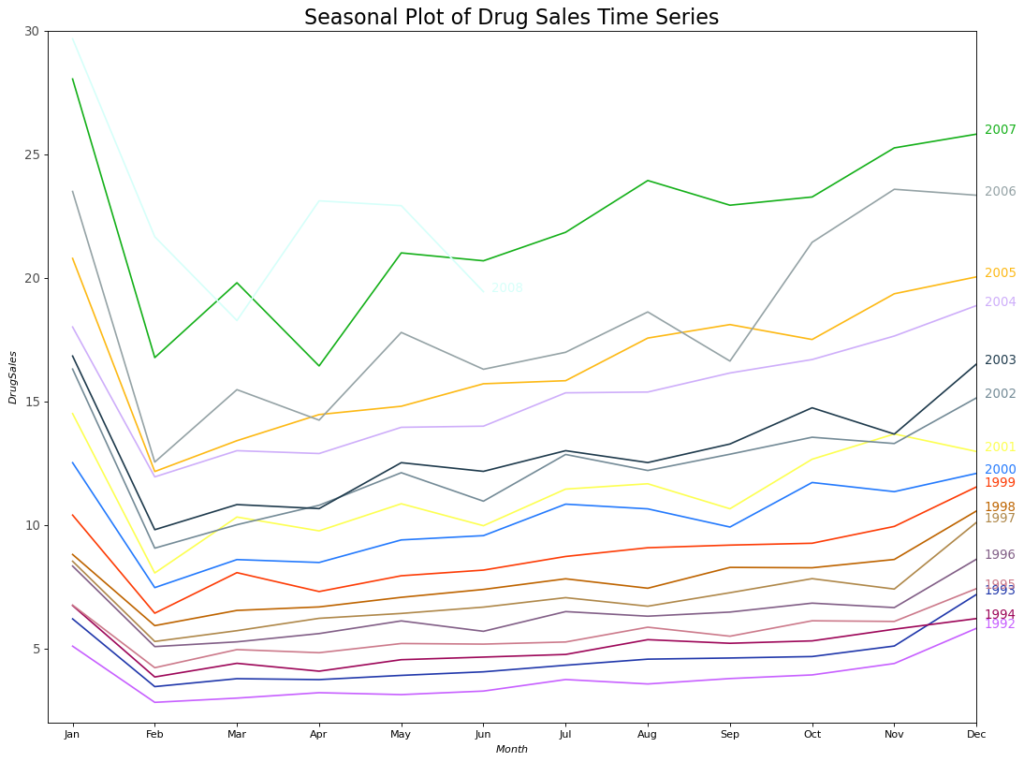
Since its a monthly time series and follows a certain repetitive pattern every year, you can plot each year as a separate line in the same plot. This lets you compare the year wise patterns side-by-side.
Seasonal Plot of a Time Series
# Import Data
df = pd.read_csv(r'C:\Users\VIVEK\Downloads/a10.csv', parse_dates=['date'], index_col='date')
df.reset_index(inplace=True)
# Prepare data
df['year'] = [d.year for d in df.date]
df['month'] = [d.strftime('%b') for d in df.date]
years = df['year'].unique()
# Prep Colors
np.random.seed(100)
mycolors = np.random.choice(list(mpl.colors.XKCD_COLORS.keys()), len(years), replace=False)
# Draw Plot
plt.figure(figsize=(16,12), dpi= 80)
for i, y in enumerate(years):
if i > 0:
plt.plot('month', 'value', data=df.loc[df.year==y, :], color=mycolors[i], label=y)
plt.text(df.loc[df.year==y, :].shape[0]-.9, df.loc[df.year==y, 'value'][-1:].values[0], y, fontsize=12, color=mycolors[i])
# Decoration
plt.gca().set(xlim=(-0.3, 11), ylim=(2, 30), ylabel='$Drug Sales$', xlabel='$Month$')
plt.yticks(fontsize=12, alpha=.7)
plt.title("Seasonal Plot of Drug Sales Time Series", fontsize=20)
Every February, medicine sales plummet, then rise in March, fall again in April, and so on. The pattern clearly repeats itself year after year.
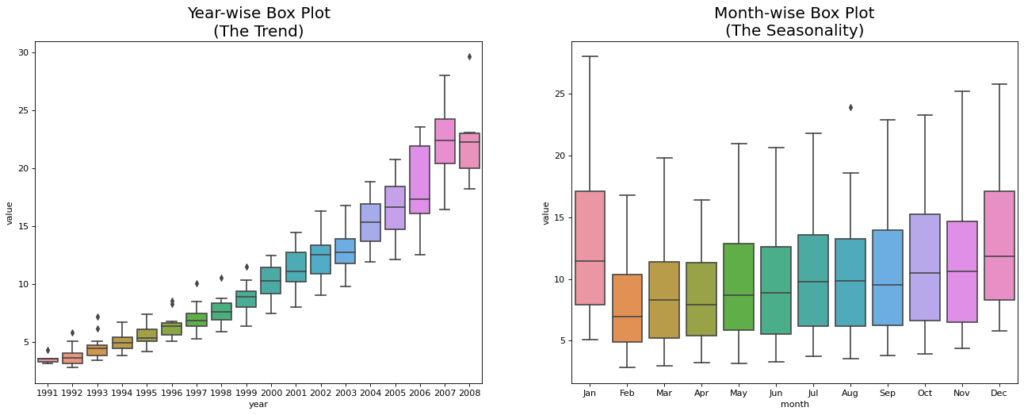
However, as the years pass, drug sales climb overall. A excellent year-by-year boxplot helps you visualize this trend and how it evolves over time. Similarly, to see the monthly distributions, create a month-by-month box plot.
Boxplot of Month-wise (Seasonal) and Year-wise (trend) Distribution
You can arrange the data at seasonal intervals to show how the values are distributed within a specific year or month, as well as how they compare across time.
# Import Data
df = pd.read_csv(r'C:\Users\VIVEK\Downloads/a10.csv', parse_dates=['date'], index_col='date')
df.reset_index(inplace=True)
# Prepare data
df['year'] = [d.year for d in df.date]
df['month'] = [d.strftime('%b') for d in df.date]
years = df['year'].unique()
# Draw Plot
fig, axes = plt.subplots(1, 2, figsize=(20,7), dpi= 80)
sns.boxplot(x='year', y='value', data=df, ax=axes[0])
sns.boxplot(x='month', y='value', data=df.loc[~df.year.isin([1991, 2008]), :])
# Set Title
axes[0].set_title('Year-wise Box Plot\n(The Trend)', fontsize=18);
axes[1].set_title('Month-wise Box Plot\n(The Seasonality)', fontsize=18)
plt.show()
The boxplots clearly show the year- and month-wise distributions. In addition, a month-by-month boxplot shows that December and January have much greater medicine sales, which can be linked to the holiday discount season.
So far, we’ve noticed enough commonalities to determine the pattern.
Patterns in a time series
Any time series can be divided into the subsequent parts: Base Level, Seasonality, Trend, and Error
When a rising or decreasing slope is seen in the time series, a trend is noted. On the other hand, seasonality is noted when a clear, recurring pattern is seen between regular intervals as a result of seasonal variables. The reason for this could be the day of the month, the weekday, the month of the year, or even the hour of the day.
All time series do not, however, have to exhibit seasonality or a trend. A time series may exhibit seasonality but lack a clear pattern. Contrarily, things can also be true.
So, a time series may be imagined as a combination of the trend, seasonality and the error terms
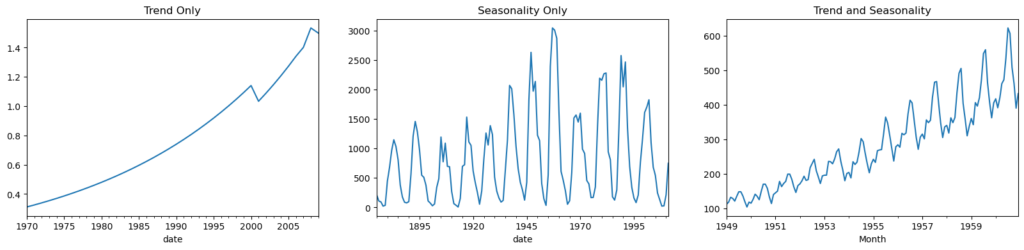
import pandas as pd
fig, axes = plt.subplots(1,3, figsize=(20,4), dpi=100)
pd.read_csv(r'C:\Users\VIVEK\Downloads/guinearice.csv', parse_dates=['date'], index_col='date').plot(title='Trend Only', legend=False, ax=axes[0])
pd.read_csv(r'C:\Users\VIVEK\Downloads/sunspotarea.csv', parse_dates=['date'], index_col='date').plot(title='Seasonality Only', legend=False, ax=axes[1])
pd.read_csv(r'C:\Users\VIVEK\Downloads/AirPassengers.csv', parse_dates=['Month'], index_col='Month').plot(title='Trend and Seasonality', legend=False, ax=axes[2])
Another aspect to consider is the cyclic behaviour. It happens when the rise and fall pattern in the series does not happen in fixed calendar-based intervals. Care should be taken to not confuse ‘cyclic’ effect with ‘seasonal’ effect.
So, How to diffentiate between a ‘cyclic’ vs ‘seasonal’ pattern?
If the patterns are not of fixed calendar based frequencies, then it is cyclic. Because, unlike the seasonality, cyclic effects are typically influenced by the business and other socio-economic factors.
Additive and multiplicative time series
Depending on the nature of the trend and seasonality, a time series can be characterized as additive or multiplicative, with each observation in the series expressed as either a sum or a product of the components:
Additive time series formula: Value = Base Level + Trend + Seasonality + Error.
Multiplicative Time Series formula: Value = Base Level x Trend x Seasonality x Error.
How to decompose a time series into its components?
A classical decomposition of a time series involves treating the series as an additive or multiplicative combination of the base level, trend, seasonal index, and residual.
This is easily accomplished using statsmodels’ seasonal_decompose function.
from statsmodels.tsa.seasonal import seasonal_decompose
from dateutil.parser import parse
# Import Data
df = pd.read_csv(r'C:\Users\VIVEK\Downloads/a10.csv', parse_dates=['date'], index_col='date')
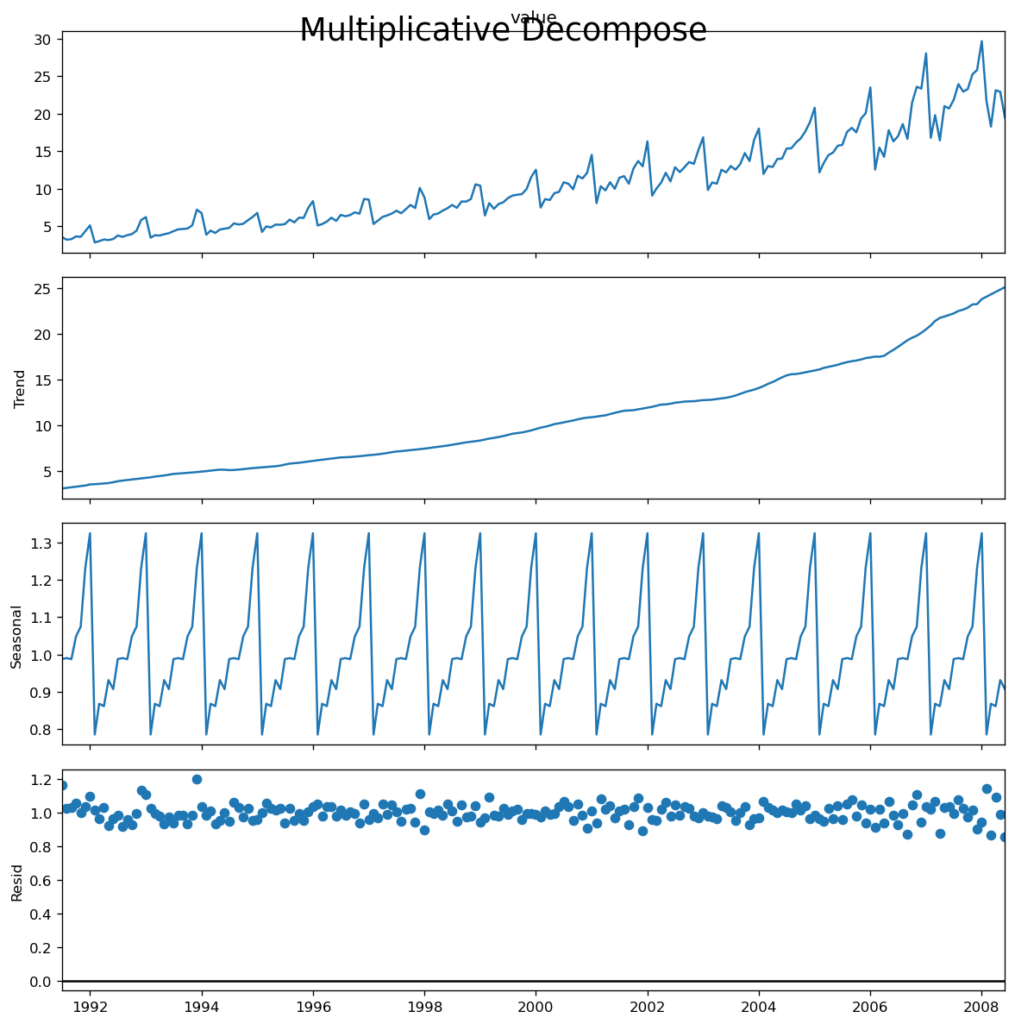
# Multiplicative Decomposition
result_mul = seasonal_decompose(df['value'], model='multiplicative', extrapolate_trend='freq')
# Additive Decomposition
result_add = seasonal_decompose(df['value'], model='additive', extrapolate_trend='freq')
# Plot
plt.rcParams.update({'figure.figsize': (10,10)})
result_mul.plot().suptitle('Multiplicative Decompose', fontsize=22)
result_add.plot().suptitle('Additive Decompose', fontsize=22)
plt.show()
Setting extrapolate_trend=’freq’ resolves any missing values in the trend and residuals at the start of the series.
If you look closely at the additive decomposition’s residuals, you’ll see several patterns. However, the multiplicative decomposition appears to be random, which is a positive thing. So, ideally, multiplicative decomposition should be used for this series.
The numerical output from the trend, seasonal, and residual components is kept in the result_mul output. Let’s extract and save them in a dataframe.
# Extract the Components ----
# Actual Values = Product of (Seasonal * Trend * Resid)
df_reconstructed = pd.concat([result_mul.seasonal, result_mul.trend, result_mul.resid, result_mul.observed], axis=1)
df_reconstructed.columns = ['seas', 'trend', 'resid', 'actual_values']
df_reconstructed.head()
If you check, the product of seas, trend and resid columns should exactly equal to the actual_values.
Stationary and Non-Stationary Time Series
Stationarity is a property of time series. A stationary series has values that do not change over time.
That is, the series’ statistical features such as mean, variance, and autocorrelation remain constant across time. The autocorrelation of the series is simply the series’ correlation with its past values; more on this coming up.
A stationary time series is free of seasonal impacts as well.
So, why is a stationary series important? Why am I even discussing it?
I’ll get to it later, but remember that almost any time series may be made stationary by applying a proper transformation. Most statistical forecasting methods are intended to function with a stationary time series. The initial step in forecasting is usually to perform a transformation to convert a non-stationary series to stationary.
How to make a time series stationary?
To make series stationary,:
- Differentiating the Series (once or more)
- Take the log of the series.
- Determine the nth root of the series.
- Combination of the above.
The most popular and convenient way for stationarizing a series is to differencing it at least once until it is nearly stationary.
So, what is differencing?
If Y_t represents the value at time ‘t’, then the initial difference in Y is Yt – Yt-1. To put it simply, differencing the series is the process of subtracting the next value from the present value.
If the first difference does not result in a stationary series, you can use the second difference. And so on.
For instance, take the following series: [1, 5, 2, 12, 20].
First differencing yields: [5-1, 2-5, 12-2, 20-12] = [4, -3, 10, 8].
Second differencing yields: [-3-4, -10-3, 8-10] = [-7, -13, -2].
Why make a non-stationary series stationary before forecasting?
Forecasting a stationary series is straightforward, and the results are more dependable.
An important reason is that autoregressive forecasting models are essentially linear regression models that use the series’ own lag(s) as predictors.
We know that linear regression performs best when the predictors (X variables) are not linked. Stationarizing the series tackles this problem by removing any persistent autocorrelation, resulting in predictors (series lags) in forecasting models that are nearly independent.
Now that we’ve established the importance of series stationarity, how do we determine whether a given series is stationary or not?
How to test for stationarity?
The stationarity of a series can be determined by looking at the plot, like we did earlier.
Another way is to divide the series into two or more contiguous pieces and calculate summary statistics such as mean, variance, and autocorrelation. If the data are significantly varied, the series is unlikely to be stationary.
Nonetheless, you need a mechanism for quantitatively determining whether a particular series is stationary or not. This can be accomplished utilizing statistical tests known as ‘Unit Root Tests’. There are several variations of this test, which determine whether a time series is non-stationary and has a unit root.
There are several implementations of Unit Root tests, including:
- Augmented Dickey Fuller Test (ADH Test)
- KPSS test (stationary trend): Kwiatkowski, Phillips, Schmidt, and Shin.
- The Philips Perron Test (PP Test)
The ADF test is the most widely used, with the null hypothesis that the time series has a unit root and is not stationary. So, if the P-value in the ADH test is less than 0.05, you reject the null hypothesis.
In contrast, the KPSS test is used to determine trend stationarity. The null hypothesis and the P-value interpretation are exactly the opposite of the ADH test. The following Python code implements these two tests using the statsmodels module.
from statsmodels.tsa.stattools import adfuller, kpss
df = pd.read_csv(r'C:\Users\VIVEK\Downloads/a10.csv', parse_dates=['date'])
# ADF Test
result = adfuller(df.value.values, autolag='AIC')
print(f'ADF Statistic: {result[0]}')
print(f'p-value: {result[1]}')
for key, value in result[4].items():
print('Critial Values:')
print(f' {key}, {value}')
# KPSS Test
result = kpss(df.value.values, regression='c')
print('\nKPSS Statistic: %f' % result[0])
print('p-value: %f' % result[1])
for key, value in result[3].items():
print('Critial Values:')
print(f' {key}, {value}')
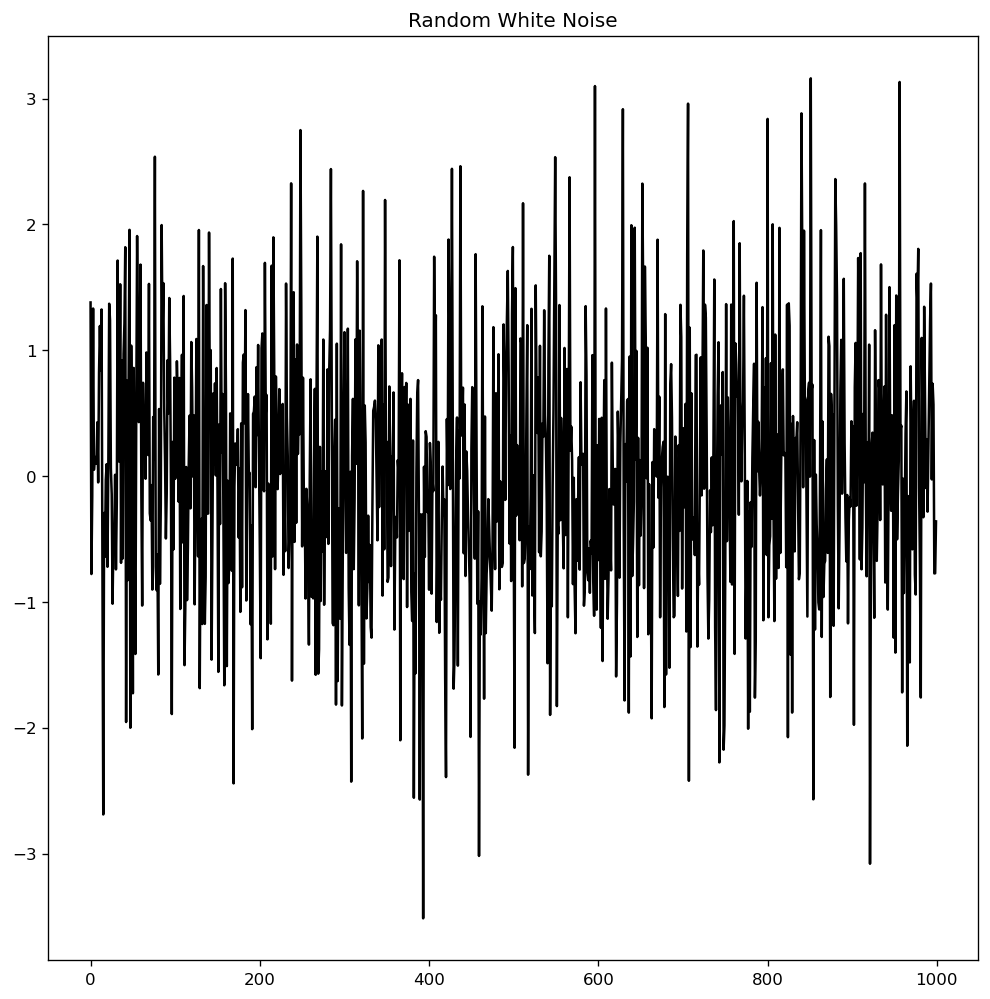
What is the difference between white noise and a stationary series?
White noise, like a stationary series, is not a function of time, which means that its mean and variance do not change with time. The distinction is that white noise is fully random, with a mean of zero.
White noise has no discernible pattern. If you think of the sound signals in an FM radio as a time series, the blank sound you hear between channels is white noise.
In mathematics, a sequence of entirely random numbers with mean zero is a white noise.
randvals = np.random.randn(1000)
pd.Series(randvals).plot(title='Random White Noise', color='k')
How to detrend a time series?
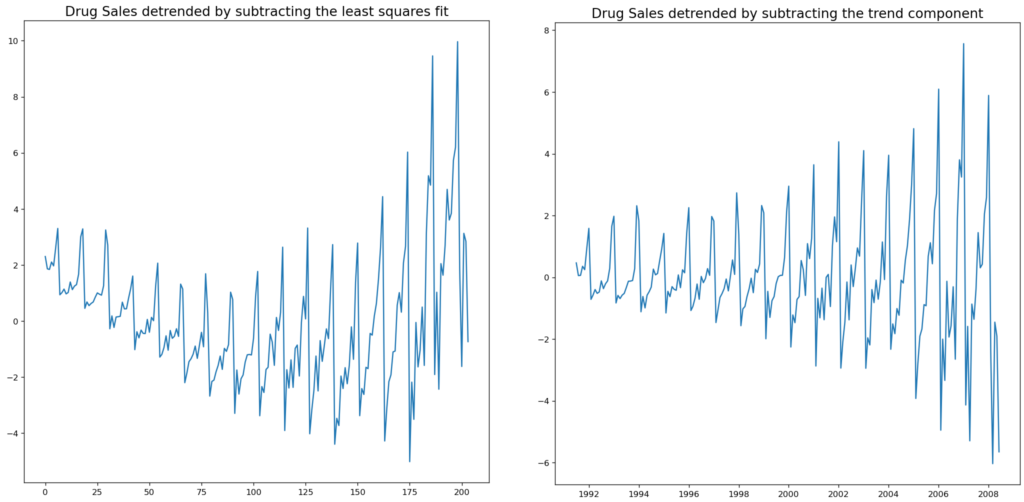
Detrending a time series is removing the trend component from the series. But how do we extract the trend? There are several approaches.
- Remove the line of best fit from the time series. A linear regression model with time steps as the predictor can provide the line of greatest fit. For more complex trends, consider using quadratic terms (x^2) in the model.
- Subtract the trend component obtained from the time series decomposition we discussed earlier.
- Subtract the mean.
- To remove moving average trend lines or cyclical components, use a filter such as the Baxter-King filter (statsmodels.tsa.filters.bkfilter) or the Hodrick-Prescott filter (statsmodels.tsa.filters.hpfilter).
Let’s implement the first two methods:
# Using scipy: Subtract the line of best fit
from scipy import signal
df = pd.read_csv(r'C:\Users\VIVEK\Downloads/a10.csv', parse_dates=['date'])
detrended = signal.detrend(df.value.values)
plt.plot(detrended)
plt.title('Drug Sales detrended by subtracting the least squares fit', fontsize=16)
# Using statmodels: Subtracting the Trend Component.
from statsmodels.tsa.seasonal import seasonal_decompose
df = pd.read_csv(r'C:\Users\VIVEK\Downloads/a10.csv', parse_dates=['date'], index_col='date')
result_mul = seasonal_decompose(df['value'], model='multiplicative', extrapolate_trend='freq')
detrended = df.value.values - result_mul.trend
plt.plot(detrended)
plt.title('Drug Sales detrended by subtracting the trend component', fontsize=16)
How to deseasonalize a time series?
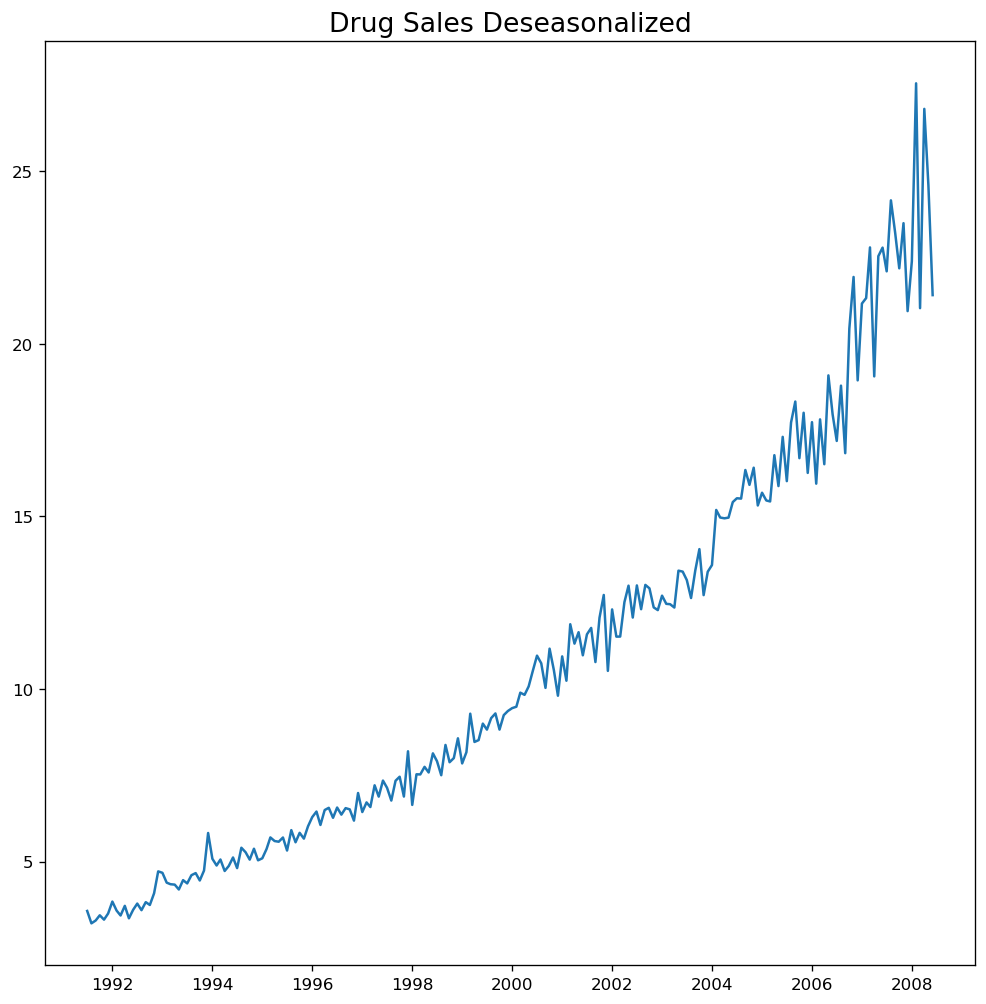
There are several methods for deseasonalizing a time series as well. Here are a few:
— 1. Use a moving average with length as the seasonal window. This will smooth out in series during the procedure.
–2. Seasonal difference of the series (subtract previous season’s value from current value).
–3. Divide the series by the seasonal index obtained by STL decomposition.
If dividing by the seasonal index does not work, consider taking a log of the series and then deseasonalizing. You can return to the original scale by taking an exponential.
# Subtracting the Trend Component.
df = pd.read_csv(r'C:\Users\VIVEK\Downloads/a10.csv', parse_dates=['date'], index_col='date')
# Time Series Decomposition
result_mul = seasonal_decompose(df['value'], model='multiplicative', extrapolate_trend='freq')
# Deseasonalize
deseasonalized = df.value.values / result_mul.seasonal
# Plot
plt.plot(deseasonalized)
plt.title('Drug Sales Deseasonalized', fontsize=16)
plt.plot()
How to test for seasonality of a time series?
The most popular method is to plot the series and look for repeatable patterns across set time periods. So, the clock or calendar determines the sorts of seasonality.
- Hour of day
- Day of month
- Weekly
- Monthly
- Yearly
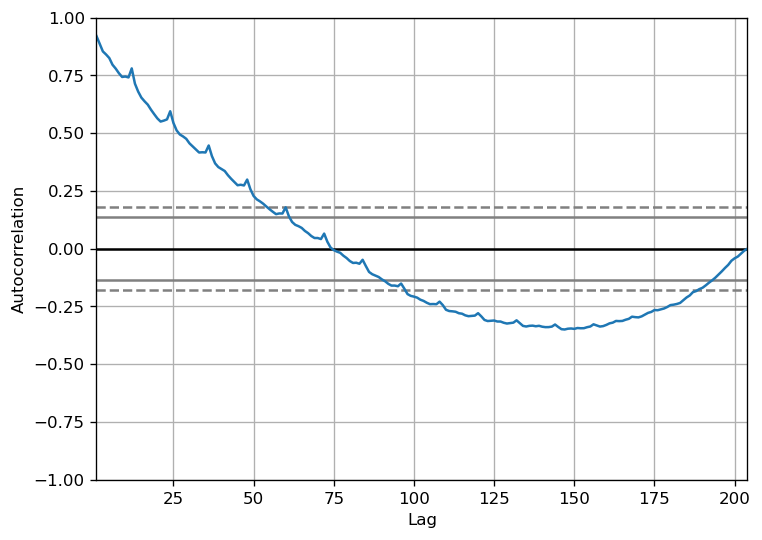
However, if you want a more definitive look at the seasonality, try the Autocorrelation Function (ACF) figure. More on the ACF in the next sections. However, when there is a significant seasonal pattern, the ACF plot frequently shows clear repeating spikes at multiples of the seasonal window.
For example, the drug sales time series is a monthly series with trends that reoccur each year. As a result, you can notice spikes at the 12th, 24th, and 36th lines.
I must warn you that in real-world datasets, such powerful patterns are rarely discovered and can be affected by any noise, so you must use a keen eye to catch these patterns.
from pandas.plotting import autocorrelation_plot
df = pd.read_csv(r'C:\Users\VIVEK\Downloads/a10.csv')
# Draw Plot
plt.rcParams.update({'figure.figsize':(7,5), 'figure.dpi':120})
autocorrelation_plot(df.value.tolist())
Alternatively, if you want to do a statistical test, the CHTest can evaluate whether seasonal differencing is required to stationarize the series.
How to treat missing values in a time series?
Your time series may have missing dates and times. That is, the data was either not gathered or not available during those time periods. It is possible that the measurement was zero on those days; in that case, you may fill in those periods with zero.
Second, when dealing with time series, it is generally not recommended to replace missing data with the series’ mean, especially if the series is not stationary. As a quick and dirty fix, you could forward-fill the previous value.
However, depending on the nature of the series, you should attempt several ways before deciding. Here are some viable alternatives to imputation:
- Backward Fill
- Linear Interpolation
- Quadratic interpolation.
- Mean of the nearest neighbors.
- Mean of seasonal couterparts.
To evaluate imputation performance, I manually inject missing values into the time series, impute them using the methods described above, and then compare the mean squared error of the imputed values to the actual values.
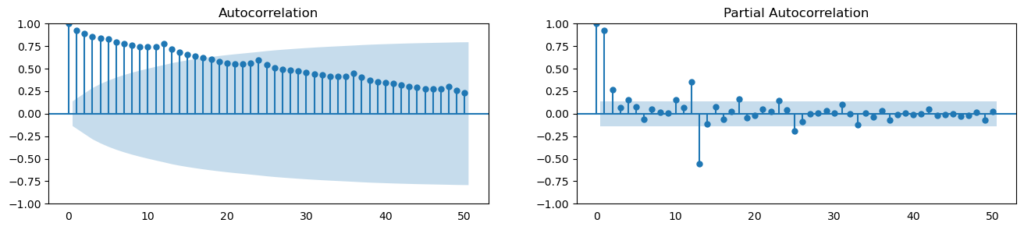
What is autocorrelation and partial autocorrelation functions?
Autocorrelation is essentially the correlation between a series and its own lags. If a series is strongly autocorrelated, it suggests that prior values (lags) can be used to forecast the current value.
Partial autocorrelation communicates comparable information, however it only conveys the series’ pure correlation and lag, removing the correlation contributions from intermediate lags.
from statsmodels.tsa.stattools import acf, pacf
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
df = pd.read_csv(r'C:\Users\VIVEK\Downloads/a10.csv')
# Calculate ACF and PACF upto 50 lags
# acf_50 = acf(df.value, nlags=50)
# pacf_50 = pacf(df.value, nlags=50)
# Draw Plot
fig, axes = plt.subplots(1,2,figsize=(16,3), dpi= 100)
plot_acf(df.value.tolist(), lags=50, ax=axes[0])
plot_pacf(df.value.tolist(), lags=50, ax=axes[1])
How to compute partial autocorrelation function?
So, how can we compute partial autocorrelation?
The partial autocorrelation of lag (k) of a series is the lag coefficient in Y’s autoregression equation. The autoregressive equation of Y is just the linear regression of Y with its own lags as predictors.
For example, if Y_t is the current series and Y_t-1 is Y’s lag 1, the partial autocorrelation of lag 3 (Y_t-3) is the coefficient of Y_t-3 in the equation below:
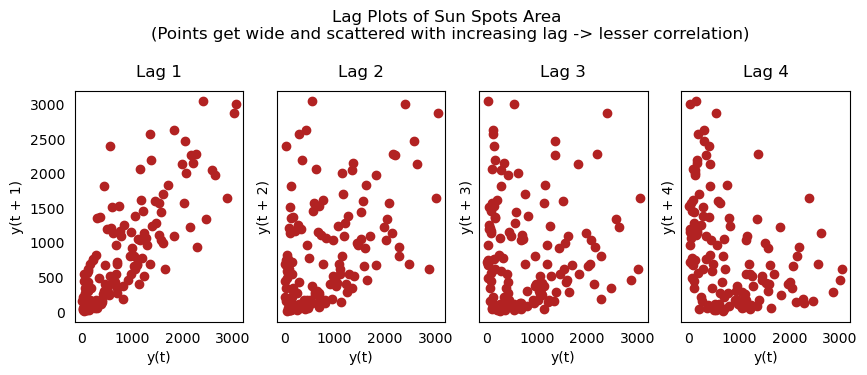
Lag Plots
A lag plot is a scatter plot that compares a time series to its own lag. It is typically used to check for autocorrelations. If the series contains a pattern like the one shown below, it is autocorrelated. If there is no such pattern, the series will most likely be random white noise.
The plots in the example below for Sunspots area time series get increasingly fragmented as n_lag grows.
from pandas.plotting import lag_plot
plt.rcParams.update({'ytick.left' : False, 'axes.titlepad':10})
# Import
ss = pd.read_csv(r'C:\Users\VIVEK\Downloads/sunspotarea.csv')
a10 = pd.read_csv(r'C:\Users\VIVEK\Downloads/a10.csv')
# Plot
fig, axes = plt.subplots(1, 4, figsize=(10,3), sharex=True, sharey=True, dpi=100)
for i, ax in enumerate(axes.flatten()[:4]):
lag_plot(ss.value, lag=i+1, ax=ax, c='firebrick')
ax.set_title('Lag ' + str(i+1))
fig.suptitle('Lag Plots of Sun Spots Area \n(Points get wide and scattered with increasing lag -> lesser correlation)\n', y=1.15)
fig, axes = plt.subplots(1, 4, figsize=(10,3), sharex=True, sharey=True, dpi=100)
for i, ax in enumerate(axes.flatten()[:4]):
lag_plot(a10.value, lag=i+1, ax=ax, c='firebrick')
ax.set_title('Lag ' + str(i+1))
fig.suptitle('Lag Plots of Drug Sales', y=1.05)
plt.show()
How to estimate the forecastability of a time series?
The more consistent and recurring patterns a time series exhibits, the easier it is to forecast. The ‘Approximate Entropy’ can be used to measure the regularity and unpredictability of fluctuations in a time series.
Forecasting becomes increasingly difficult as the estimated entropy increases.
Another better alternate is the ‘Sample Entropy’.
Sample entropy is comparable to approximation entropy, however it is more reliable in calculating complexity for short time series. For example, a random time series with fewer data points may have lower ‘approximate entropy’ than a more’regular’ time series, whereas a longer random time series will have higher ‘approximate entropy’.
This is a problem that Sample Entropy effectively addresses. View the demonstration below.
# https://en.wikipedia.org/wiki/Approximate_entropy
ss = pd.read_csv(r'C:\Users\VIVEK\Downloads/sunspotarea.csv')
a10 = pd.read_csv(r'C:\Users\VIVEK\Downloads/a10.csv')
rand_small = np.random.randint(0, 100, size=36)
rand_big = np.random.randint(0, 100, size=136)
def ApEn(U, m, r):
"""Compute Aproximate entropy"""
def _maxdist(x_i, x_j):
return max([abs(ua - va) for ua, va in zip(x_i, x_j)])
def _phi(m):
x = [[U[j] for j in range(i, i + m - 1 + 1)] for i in range(N - m + 1)]
C = [len([1 for x_j in x if _maxdist(x_i, x_j) <= r]) / (N - m + 1.0) for x_i in x]
return (N - m + 1.0)**(-1) * sum(np.log(C))
N = len(U)
return abs(_phi(m+1) - _phi(m))
print(ApEn(ss.value, m=2, r=0.2*np.std(ss.value))) # 0.651
print(ApEn(a10.value, m=2, r=0.2*np.std(a10.value))) # 0.537
print(ApEn(rand_small, m=2, r=0.2*np.std(rand_small))) # 0.143
print(ApEn(rand_big, m=2, r=0.2*np.std(rand_big))) # 0.716
Why and How to smoothen a time series?
- Smoothing a time series can help reduce noise in signals. Obtain a good approximation of the noise-filtered series.
Smoothed versions of series might be used as features to explain the original series.
Better visualize the underlying trend.
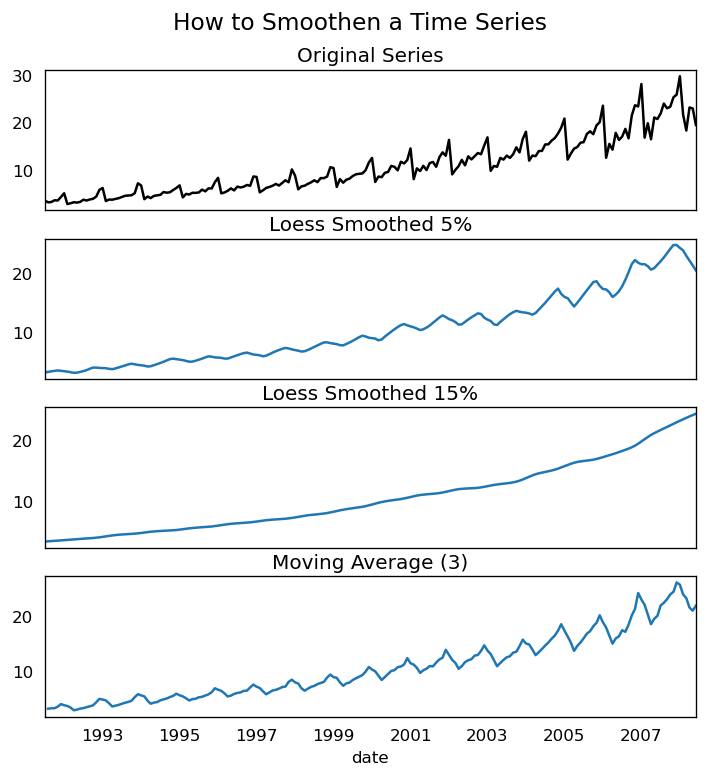
So how can you smooth a series? Let us discuss the following methods: - Take a moving average.
- Perform LOESS smoothing (Localized Regression).
- Perform a LOWESS smoothing (Locally Weighted Regression).
Moving average is just the average of a rolling window with a set width. However, you must set the window width carefully, as a huge window size would over-smooth the series. For example, a window size equal to the seasonal period (e.g., 12 for a month-by-month series) effectively eliminates the seasonal effect.
LOESS (‘LOcalized regrESSion’) fits multiple regressions in the local neighborhood of each point. It is implemented in the statsmodels package, and you may regulate the degree of smoothing with the frac argument, which defines the proportion of neighboring data points that should be included while fitting a regression model.
from statsmodels.nonparametric.smoothers_lowess import lowess
plt.rcParams.update({'xtick.bottom' : False, 'axes.titlepad':5})
# Import
df_orig = pd.read_csv(r'C:\Users\VIVEK\Downloads/a10.csv', parse_dates=['date'], index_col='date')
# 1. Moving Average
df_ma = df_orig.value.rolling(3, center=True, closed='both').mean()
# 2. Loess Smoothing (5% and 15%)
df_loess_5 = pd.DataFrame(lowess(df_orig.value, np.arange(len(df_orig.value)), frac=0.05)[:, 1], index=df_orig.index, columns=['value'])
df_loess_15 = pd.DataFrame(lowess(df_orig.value, np.arange(len(df_orig.value)), frac=0.15)[:, 1], index=df_orig.index, columns=['value'])
# Plot
fig, axes = plt.subplots(4,1, figsize=(7, 7), sharex=True, dpi=120)
df_orig['value'].plot(ax=axes[0], color='k', title='Original Series')
df_loess_5['value'].plot(ax=axes[1], title='Loess Smoothed 5%')
df_loess_15['value'].plot(ax=axes[2], title='Loess Smoothed 15%')
df_ma.plot(ax=axes[3], title='Moving Average (3)')
fig.suptitle('How to Smoothen a Time Series', y=0.95, fontsize=14)
plt.show()