STEP BY STEP GUIDE FOR STATISTICS FOR DATA ANALYTICS
In data analytics, statistics is essential because it offers methods and tools for understanding and translating data. Here are some essential statistical ideas that are frequently applied in data analytics:
•Descriptive Statistics
•Inferential Statistics
•Probability
•Sampling Methods
•Correlation and Regression:
•Data Distributions
•Hypothesis Testing
Table of Contents
ToggleDescriptive Statistics,
Descriptive Statistics,
The primary properties of a dataset have been identified and described using descriptive statistics. They give a brief overview of the data, enabling analysts to understand its distribution, change, and core a pattern. The following are a few typical metrics in descriptive statistics:
Descriptive statistics
- Measures of Central Tendency:
- Measures of Variability
- Measures of Shape and Distribution
- Percentiles
- Range
- Frequency
- istribution
Measures of Central Tendency
Measures of Central Tendency
are employed to identify the average or centre value within a dataset. The “centre” of the data distribution is represented by a single value that they offer. The three standard central tendency measures
- Mean
- Median
- Mode
Mean
Mean:
Consider the following dataset representing the scores of 10 students on a test:
{85, 90, 78, 92, 88, 95, 82, 86, 91, 89}. To find the mean, we sum up all the values and divide by the total number of observations:
(85 + 90 + 78 + 92 + 88 + 95 + 82 + 86 + 91 + 89) / 10 = 876 / 10 = 87.6. Therefore, the mean score is 87.6.
Median:
Median:
Let’s consider the same dataset as above:
{85, 90, 78, 92, 88, 95, 82, 86, 91, 89}.
To find the median, we first arrange the values in ascending order:
78, 82, 85, 86, 88, 89, 90, 91, 92, 95. Since there are 10 observations, the median is the middle value, which is the 5th value, 88. Therefore, the median score is 88.
Mode:
Mode:
Take a look at the dataset below, which shows the number of pets that each home in a neighbourhood owns
{0, 1, 2, 2, 3, 1, 4, 0, 2, 1}.
To find the mode, we identify the value(s) that occur most frequently. In this case, both 1 and 2 occur three times, which makes them the modes of the dataset.
Therefore, the modes for this dataset are 1 and 2.
Measures of Variability
Let’s use a sample dataset to describe metrics of variability:
Look at the dataset below, which shows the ages of 10 people: {20, 25, 22, 28, 30, 21, 24, 27, 26, 23}.
- Variance:
- Standard Deviation
Add Your Heading Text Here
VARANCE
Calculate the mean:
(165 + 170 + 172 + 168 + 175 + 169 + 171 + 174) / 8 = 1374 / 8 = 171.75.
1.Subtract the mean from each value and square the differences:
(165 – 171.75)^2, (170 – 171.75)^2, (172 – 171.75)^2, (168 – 171.75)^2, (175 – 171.75)^2, (169 – 171.75)^2, (171 – 171.75)^2, (174 – 171.75)^2.
2.The squared differences are: (39.0625, 3.0625, 0.5625, 12.5625, 14.0625, 5.0625, 0.5625, 6.0625).
3.Calculate the sum of these squared differences:
39.0625 + 3.0625 + 0.5625 + 12.5625 + 14.0625 + 5.0625 + 0.5625 + 6.0625 = 81.4375.
4.Divide the sum by the total number of observations minus 1 (8 – 1 = 7)
5.to get the sample variance:
81.4375 / 7 = 11.6339285714.
Standard deviation
1.Calculate the variance (as explained in the previous response): Variance = 11.6339 square centimeters.
2.Take the square root of the variance to obtain the standard deviation: Square root of 11.6339 ≈ 3.4112.
Therefore, the standard deviation of the dataset is approximately 3.4112 centimeters.
- Standard deviation measures the dispersion or spread of data points around the mean. In this example, the standard deviation indicates the average distance between each height
Measures of Shape and Distribution:
Measures of Shape and Distribution:
Shape and distribution metrics give information about the distributional properties of a dataset. They aid in understanding the data’s uniformity, specific form, and tail behavior. Here are some typical metrics for distribution and shape:
- Skewness:
- Kurtosis:
Skewness:
Skewness:
Positive Skewness:
Consider a dataset with the following values for the income levels of a population’s members (in thousands of dollars): 20, 25, 30, 35, 40, 45, 50, and 150.
Positive skewness is indicated by the distribution’s right-side longer tail.
The majority of people’s incomes are concentrated in the lower range, whereas only a small number of people have much higher wages.
In this positively skewed distribution, the mean income is higher than the median income.
Negative Skewness:
Let’s consider a dataset representing the waiting times (in minutes) at a doctor’s office:
{50, 40, 30, 20, 15, 10, 5, 1}.
The distribution has a longer tail on the left side, indicating negative skewness.
Most individuals experience shorter waiting times, with a few outliers experiencing longer waiting times.
The mean waiting time is lower than the median waiting time in this negatively skewed distribution.
Skewness of Zero:
Consider a dataset representing the heights (in centimeters) of individuals in a sample:
{160, 165, 170, 175, 180, 185}.
1.The distribution is symmetric, with no significant imbalance in the tails.
2.The data is equally distributed around the mean, and there are no substantial skewness effects.
These examples illustrate the concept of skewness in different datasets. Positive skewness indicates a longer or fatter tail on the right side, negative skewness indicates a longer or fatter tail on the left side, and skewness of zero suggests a symmetric distribution.
Kurtosis
Kurtosis
*Consider a dataset representing the returns (in percentages) of a stock over a certain period: {-3, 2, 1, -1, 0, 1, 4, 2}.
To calculate the kurtosis:
Calculate the mean:
(-3 + 2 + 1 + -1 + 0 + 1 + 4 + 2) / 8 = 6 / 8 = 0.75.
Calculate the variance:
Variance = [(1/8) * ((-3 – 0.75)^2 + (2 – 0.75)^2 + (1 – 0.75)^2 + (-1 – 0.75)^2 + (0 – 0.75)^2 + (1 – 0.75)^2 + (4 – 0.75)^2 + (2 – 0.75)^2)] ≈ 4.875.
Calculate the fourth moment:
Fourth Moment = [(1/8) * ((-3 – 0.75)^4 + (2 – 0.75)^4 + (1 – 0.75)^4 + (-1 – 0.75)^4 + (0 – 0.75)^4 + (1 – 0.75)^4 + (4 – 0.75)^4 + (2 – 0.75)^4)] ≈ 33.7969.
Calculate the kurtosis:
Kurtosis = (Fourth Moment / Variance^2) – 3 ≈ (33.7969 / (4.875^2)) – 3 ≈ 0.9796.
Therefore, the kurtosis of the dataset is approximately 0.9796.
Kurtosis measures the peakedness or flatness of a distribution compared to a normal distribution. In this example, the positive kurtosis value suggests that the distribution has a sharper peak and heavier tails compared to a normal distribution. It indicates a higher likelihood of extreme returns or outliers in the dataset.
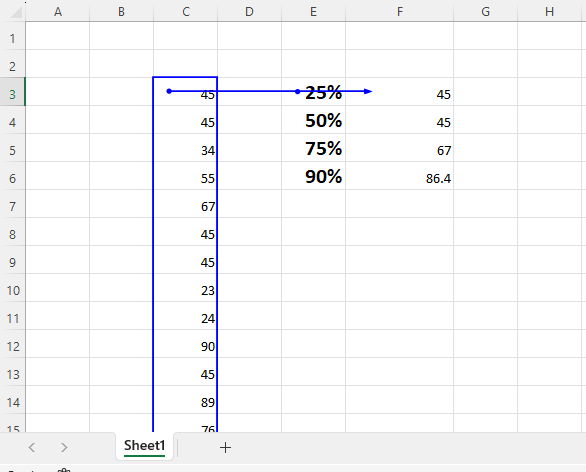
Percentile :
Percentile :
75th percentile is the value below which 75% of the data falls. This means that 75% of the data values in the dataset are less than or equal to the 75th
Range
Range, an easy measure of variability, shows the difference between a dataset’s highest and minimum values. It gives an elementary understanding of how the data are distributed.
Use these steps to determine a dataset’s range:
The dataset should be sorted ascending.
Take the least value and subtract it from the maximum value.
Range
For example, consider the following dataset representing the heights (in centimeters) of a group of individuals: {160, 165, 170, 175, 180, 185}.
To calculate the range:
Sort the dataset in ascending order: {160, 165, 170, 175, 180, 185}.
Subtract the minimum value (160) from the maximum value (185):
Range = 185 – 160 = 25.
Therefore, the range of the dataset is 25 centimeters. It indicates that there is a 25-centimeter difference between the tallest and shortest individuals in the group.
While the range provides a simple measure of variability, it has limitations as it only considers the extremes of the dataset. It does not provide information about the distribution or variability within the dataset. Other measures, such as variance and standard deviation, offer more comprehensive insights into the spread of data.
Frequency Distribution
Consider the following dataset representing the scores of students in a class: {75, 80, 65, 70, 85, 90, 75, 80, 75, 85, 80, 70, 75}.
To create a frequency distribution table:
Sort the dataset in ascending order: {65, 70, 70, 75, 75, 75, 75, 80, 80, 80, 85, 85, 90}.
Identify the unique values in the dataset and determine their frequencies (number of occurrences).
Frequency Distribution
Count how many times each value appears in the dataset.
Value | Frequency
65 | 1
70 | 2
75 | 4
80 | 3
85 | 2
90 | 1
This frequency distribution table shows the unique values in the dataset and their corresponding frequencies. For example, the value 75 appears four times, while the values 65 and 90 appear only once.
Frequency distribution tables provide a summary of the distribution of values in a dataset. They help identify the most common values and provide an overview of the frequency or occurrence of different values. This information can be useful for further analysis and understanding of the dataset.
Inferential Statistics
Inferential statistics is an area of statistics that deals with making inferences or conclusions about a wider population based on sample data. It helps investigators in generalizing from small data sets and making predictions. Here is an illustration of the idea of inferential statistics:
Let’s imagine a business wishes to gauge how satisfied its staff members are with their jobs. There are 10,000 people working for the company. They choose to get information from a randomly selected sample of 500 employees rather than conducting time-consuming and unrealistic surveys of every employee.
Sampling:
Out of a total workforce of 10,000 employees, 500 are chosen at random by the corporation. By doing this, bias in the sample is diminished and every employee has an equal chance of getting chosen.
Data collection:
A job satisfaction survey is given to the 500 employees that were chosen. The survey includes inquiries about respondents’ general job satisfaction, work-life balance, pay, chances for career advancement, and other pertinent issues.
s.
Descriptive Statistics
In order to summarise the sample data, descriptive statistics are utilised. For the 100 cars in the sample, the manufacturer computes the mean, median, and standard deviation of the fuel efficiency figures.
Inferential Statistics:
Based on the sample data, inferential statistics are used to make inferences about the typical fuel efficiency of the 1,000 cars.
Confidence Intervals:
To determine the range within which the actual population mean fuel economy lies, the manufacturer calculates a confidence interval, such as a 95% confidence interval. Suppose they discover that the sample’s average fuel economy is 50 MPG, with a 95% confidence range ranging from 48 MPG to 52 MPG. Since the genuine population mean fuel efficiency falls within this range, they may be 95% confident in this.
Example
Let’s use an example to calculate inferential statistics. Let’s say we’ve gathered the MPG (miles per gallon) information for a sample of 50 cars. These are the data:
45, 42, 50, 48, 43, 47, 52, 55, 49, 51, 46, 44, 53, 47, 49, 48, 50, 45, 46, 52, 50, 48, 45, 47, 51, 49, 52, 54, 46, 47, 49, 48, 50, 45, 43, 51, 48, 50, 47, 49, 46, 52, 49, 44, 47, 48, 51, 50, 48, 46, 49, 51.
Step 1: Descriptive Statistics
Let’s figure out the sample’s mean, median, and standard deviation.
The sum of all the values divided by the total number of values is the mean.
Sum = 2,417
Mean = Sum / Number of values = 2,417 / 50 = 48.34 MPG
Median: Arrange the values in ascending order and find the middle value:
42, 43, 43, 44, 45, 45, 45, 46, 46, 46, 46, 47, 47, 47, 47, 47, 48, 48, 48, 48,
48, 48, 48, 49, 49, 49, 49, 49, 49, 49, 50, 50, 50, 50, 50, 51, 51, 51, 51, 52,
52, 52, 52, 53, 54, 55
Median = 48 MPG
Standard Deviation:
Calculate the standard deviations for each value:
Value – Mean equals deviation
We determine the deviations using the example data in the manner shown below:
(-3.34), (-6.34), 1.66, (-0.34), (-5.34), (-1.34), 3.66, 6.66, 0.66, 2.66,
(-2.34), (-4.34), 4.66, (-1.34), 0.66, (-0.34), 1.66, (-3.34), (-2.34), 3.66,
1.66, (-0.34), (-3.34), (-1.34), 2.66, 0.66, 3.66, 5.66, (-2.34), (-1.34),
0.66, (-0.34), 1.66, (-3.34), (-5.34), 2.66, (-0.34), 1.66, (-1.34), 0.66,
(-2.34), 3.66, 0.66, (-4.34), (-1.34), 0.66, (-0.34), 2.66, 1.66, (-0.34),
(-2.34), 0.66, 2.66.
Square each deviation:
Squared Deviation = Deviation^2
Squaring each deviation, we have:
11.1556, 40.1956, 2.7556, 0.1156, 28.5156, 1.7956, 13.4356, 44.3556,
0.4356, 7.0756, 5.4756, 18.8356, 21.5956, 1.7956, 0.4356, 0.1156, 2.7556,
11.1556, 5.4756, 13.4356, 2.7556, 0.1156, 11.1556, 1.7956, 7.0756, 0.4356,
13.4356, 32.1156, 5.4756, 1.7956, 0.4356, 2.7556, 11.1556, 28.5156, 0.1156,
2.7556, 1.7956, 0.4356, 0.1156, 5.4756, 13.4356, 0.4356, 18.8356, 1.7956,
0.4356, 0.1156, 7.0756, 2.7556, 0.1156, 5.4756, 0.4356, 7.0756.
Calculate the sum of squared deviations:
Sum of Squared Deviations = Σ(Squared Deviation)
Adding up the squared deviations, we get:
Sum of Squared Deviations = 581.92
Divide the sum of squared deviations by the number of values:
Variance = Sum of Squared Deviations /
Probability
Probability is a fundamental concept in statistics and data analytics that deals with the likelihood or chance of events occurring. It quantifies the uncertainty associated with outcomes and enables us to make predictions and make informed decisions based on data.
Here are some key topics typically covered in a probability section:
Introduction to Probability:
- Basic definitions and concepts, including sample space, events, and outcomes.
- Theoretical, experimental, and subjective approaches to probability.
- The relationship between probability and frequency.
Probability Laws and Rules:
- Addition rule: Union of events, mutually exclusive events, and non-mutually exclusive events.
- Multiplication rule: Intersection of events, independent events, and dependent events.
Complementary events and the complement rule.
Probability Distributions:
- Discrete probability distributions: Definition and properties.
- Probability mass function (PMF) and cumulative distribution function (CDF).
- Examples of common discrete distributions: Bernoulli, binomial, geometric, and Poisson.
Continuous Probability Distributions:
- Continuous probability distributions:Definition and properties.
- Probability density function (PDF) and cumulative distribution function (CDF).
- Examples of common continuous distributions: uniform, normal (Gaussian), exponential, and gamma.
Joint Probability and Conditional Probability:
- Joint probability of two or more events.
- Conditional probability and its interpretation.
- Bayes’ theorem and its applications.
Expected Value and Variance:
- Expected value (mean) and variance of a random variable.
- Properties of expected value and variance.
- Covariance and correlation.
- Random Variables and Probability Models:
Definition of random variables.
- Discrete and continuous random variables.
- Probability mass function (PMF) and probability density function (PDF) for random variables.
Sampling and Sampling Distributions:
- Random sampling and its importance.
- Sampling distributions: sampling distribution of the sample mean and the central limit theorem.
- Standard error and confidence intervals.
Law of Large Numbers and the Central Limit Theorem:
- Law of Large Numbers and its Implications.
- Central Limit Theorem and its Applications.
- Sampling from any population distribution.
Applications of Probability in Data Analytics:
- Probability in hypothesis testing.
- Probability in statistical modeling and inference.
- Probability in machine learning algorithms.
This is a general overview of the topics covered in a probability section. The level of depth and complexity can vary depending on the course or program. It’s important to practice solving probability problems and working with probability distributions to gain a solid understanding of the subject.

