Mastering Machine Learning: The Top 10 Algorithms You Need to Know
In today’s data-driven world, machine learning has become an indispensable tool for extracting valuable insights from vast amounts of data. However, for beginners entering the realm of machine learning, the plethora of algorithms available can seem overwhelming. Understanding the fundamental algorithms is crucial for building a strong foundation in this field.

Table of Contents
ToggleLinear Regression
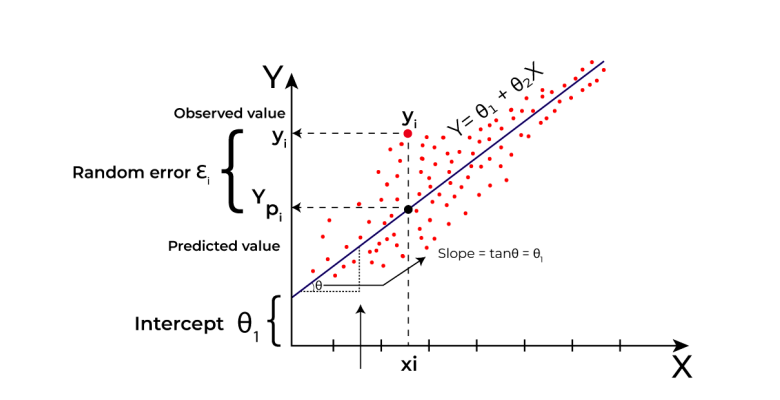
Linear regression is a statistical method used in machine learning to predict continuous outcomes or values based on input features. Let’s break down how linear regression works in simple steps:
Understanding the Concept:
Imagine you have some data where you know the input (like the size of a house) and the output (like the price of the house). Linear regression helps us find the relationship between these inputs and outputs.
Plotting the Data:
We start by plotting our data points on a graph, with the input values on the x-axis and the corresponding output values on the y-axis. This gives us a scatterplot of our data points.
Drawing a Line:
Linear regression finds the best-fitting line through the data points. This line represents the relationship between the input and output variables. The goal is to find the line that minimizes the difference between the actual data points and the predicted values on the line.
The Equation of the Line:
The equation of the line in linear regression is represented as:
Y = mX + c
Y represents the predicted output value.
X represents the input feature.
m is the slope of the line, which represents how much the output value changes for a one-unit change in the input feature.
c is the y-intercept, which represents the value of Y when X is 0.
Finding the Best-Fitting Line:
Linear regression uses a method called least squares to find the best-fitting line. It calculates the sum of the squares of the vertical distances between the data points and the line. The line that minimizes this sum is considered the best-fitting line.
Making Predictions:
Once we have the equation of the best-fitting line, we can use it to make predictions. Given a new input value, we can plug it into the equation to predict the corresponding output value.
Evaluating the Model:
Finally, we evaluate the performance of our linear regression model by comparing the predicted values to the actual values in our dataset. Common evaluation metrics include mean squared error (MSE) or R-squared.
Extensions to Complex Models:
While linear regression is simple and easy to understand, it forms the basis for more complex regression techniques like polynomial regression, ridge regression, or lasso regression, which can handle more intricate relationships between variables.
In summary, linear regression is a powerful tool for predicting continuous values based on input features. By finding the best-fitting line through the data points, it allows us to understand and quantify relationships between variables in our dataset.
Logistic regression
Logistic regression is a fundamental algorithm in machine learning, primarily used for binary classification problems. Let’s delve into how logistic regression works step by step, explained in simple terms:
Binary Classification:
Binary classification means we have two possible outcomes for our prediction: yes or no, 0 or 1, true or false. For example, predicting whether an email is spam or not spam, whether a transaction is fraudulent or legitimate, etc.
Understanding Probability:
Logistic regression predicts the probability of one of the two outcomes occurring. Instead of directly predicting 0 or 1, it predicts a probability value between 0 and 1.
Sigmoid Function:
Logistic regression uses a special function called the sigmoid function (also known as the logistic function). This function maps any real-valued number to a value between 0 and 1. The formula for the sigmoid function is:
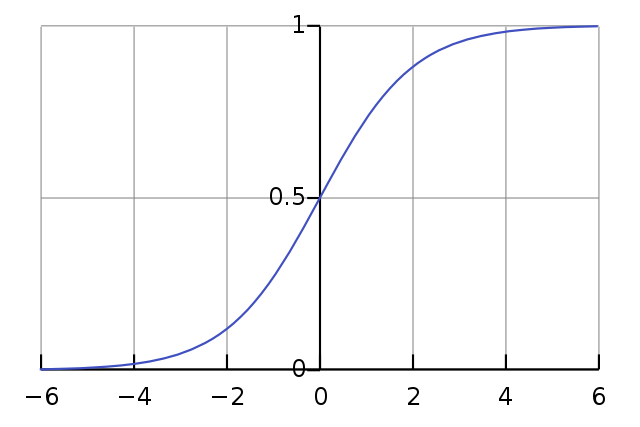
Here, “x” represents the input value, and “σ(x)” represents the output, which is the probability of the event occurring.
Linear Equation:
Like linear regression, logistic regression also has an equation, but it’s slightly different. Instead of a straight line, logistic regression uses a line that’s curved due to the sigmoid function. The equation looks like this:
Logistic Regression Equation
Here, “z” represents the linear combination of input features and their respective coefficients, just like in linear regression.
Probability Interpretation:
Once we have the output from the sigmoid function (which is a probability), we can interpret it as follows: if the probability is closer to 0, it means the event is less likely to occur, and if it’s closer to 1, it means the event is more likely to occur.
Decision Boundary:
Logistic regression separates the input space into two regions using a decision boundary. If the probability is above a certain threshold (usually 0.5), we predict one class (e.g., 1), and if it’s below the threshold, we predict the other class (e.g., 0).
Training the Model:
During training, logistic regression adjusts its coefficients to minimize the difference between the predicted probabilities and the actual outcomes in the training data. It does this using optimization algorithms like gradient descent.
Evaluation:
To evaluate the logistic regression model, we use metrics like accuracy, precision, recall, F1 score, etc., depending on the specific problem and requirements.
In summary, logistic regression is a powerful algorithm for binary classification problems, predicting the probability of an event occurring and making decisions based on that probability.
Decision Trees
Decision trees are versatile and intuitive models used in machine learning for both classification and regression tasks. Let’s explore how decision trees work in a step-by-step manner, emphasizing their simplicity and interpretability:
Intuitive Representation:
Decision trees mimic the human decision-making process by breaking down complex decision-making into a series of simple questions. Each node in the tree represents a decision based on a feature, and each branch represents the possible outcomes of that decision.
Feature Space Partitioning:
Decision trees partition the feature space into regions by recursively splitting the data based on feature values. At each step, the algorithm selects the feature that best separates the data into distinct classes or groups.
Splitting Criteria:
The decision tree algorithm evaluates different splitting criteria to determine the best feature and threshold for splitting the data at each node. Common splitting criteria include Gini impurity for classification tasks and mean squared error for regression tasks.
Building the Tree:
The decision tree algorithm continues to split the data recursively until certain stopping criteria are met, such as reaching a maximum depth, minimum number of samples per leaf node, or no further improvement in purity or error reduction.
Leaf Nodes:
Once the data is partitioned into homogeneous subsets or reaches the stopping criteria, the algorithm assigns a class label (for classification) or predicts a continuous value (for regression) at the leaf nodes of the tree.
Interpretability:
One of the key advantages of decision trees is their interpretability. The decision rules at each node can be easily understood and visualized, making it straightforward to interpret the model’s predictions and understand the factors influencing them.
Handling Categorical and Numerical Features:
Decision trees can handle both categorical and numerical features without requiring feature scaling or one-hot encoding. They automatically select the best split points for numerical features and perform multiway splits for categorical features.
Handling Missing Values:
Decision trees can handle missing values in the dataset by selecting the best split based on the available data, allowing for robust performance in real-world datasets with incomplete information.
Ensemble Methods:
Decision trees can be combined into ensemble methods such as random forests and gradient boosting, further improving predictive performance and generalization while retaining interpretability to some extent.
In summary, decision trees are powerful and intuitive models that partition the feature space into regions, making them suitable for both classification and regression tasks. Their simplicity, interpretability, and ability to handle a variety of data types make them a popular choice in many machine learning applications.
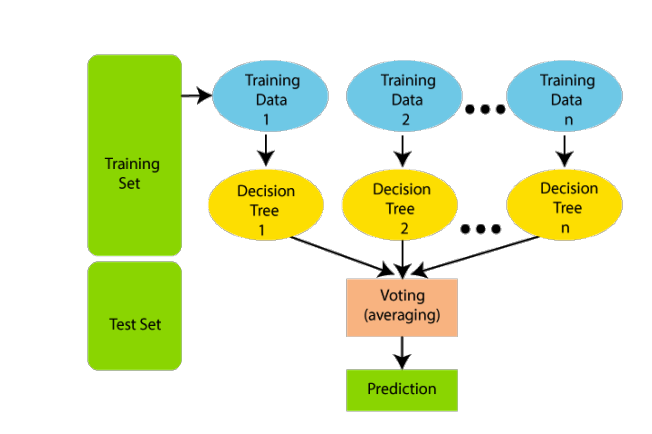
Random Forest
Random Forest is a robust and versatile ensemble learning technique that leverages the power of multiple decision trees to enhance predictive accuracy and mitigate overfitting. Here’s an explanation of how Random Forest works:
Ensemble Learning:
Random Forest belongs to the family of ensemble learning algorithms. Ensemble learning combines the predictions of multiple individual models to produce a more accurate and robust final prediction.
Construction of Decision Trees:
Random Forest constructs a predefined number of decision trees, typically referred to as “trees” or “estimators”. Each decision tree is built using a random subset of the training data and a random subset of the features.
Randomness and Diversity:
The randomness introduced in building individual trees helps to create diversity among them. Each tree may focus on different subsets of features and data instances, capturing different aspects of the underlying patterns in the data.
Bagging (Bootstrap Aggregating):
Random Forest employs a technique called bagging, where each decision tree is trained on a bootstrap sample of the training data. Bootstrap sampling involves randomly selecting data points with replacement, allowing some instances to be selected multiple times and others not at all.
Feature Randomness:
In addition to using bootstrap samples, Random Forest also introduces randomness in feature selection for each split of the decision tree. Instead of considering all features at each split, a random subset of features is considered, further enhancing diversity among the trees.
Combining Predictions:
Once all the decision trees are trained, Random Forest combines their predictions to make the final prediction. For classification tasks, it typically uses a majority voting scheme, where the class predicted by the majority of trees is chosen. For regression tasks, it averages the predictions made by individual trees.
Advantages of Random Forest:
Random Forest is highly resistant to overfitting due to the averaging effect of multiple trees.
It performs well on a wide range of datasets and can handle high-dimensional feature spaces.
Random Forest provides estimates of feature importance, allowing insights into the relative importance of different features in making predictions.
Hyperparameters:
Random Forest has several hyperparameters that can be tuned to optimize performance, such as the number of trees, maximum depth of trees, and the number of features considered at each split.
In summary, Random Forest is a powerful ensemble learning technique that combines the predictions of multiple decision trees to achieve higher accuracy and reduce the risk of overfitting, making it a popular choice for various machine learning tasks.
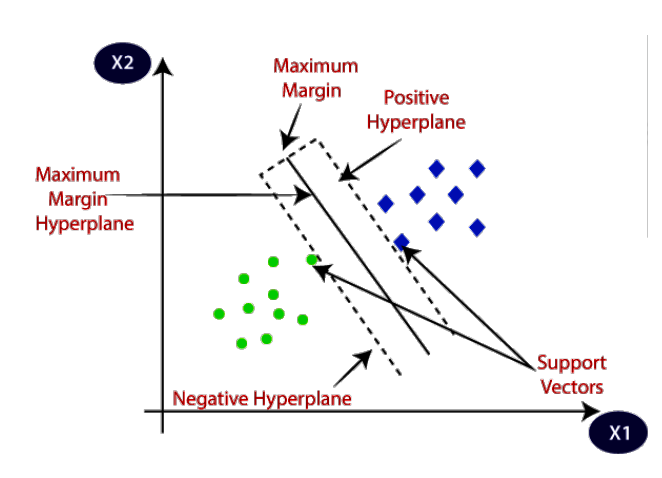
Support Vector Machines (SVM)
Support Vector Machines (SVM) is a versatile machine learning algorithm used for both classification and regression tasks. Let’s break down how SVM works:
Classification and Regression:
SVM can be used for both classification and regression tasks. In classification, SVM aims to classify data points into different categories, while in regression, it predicts continuous outcomes.
Hyperplane:
At the core of SVM is the concept of a hyperplane, which is a decision boundary that separates different classes in the feature space. For a binary classification problem, the hyperplane is a line in two dimensions, a plane in three dimensions, and a hyperplane in higher dimensions.
Maximizing Margin:
SVM finds the hyperplane that maximizes the margin, which is the distance between the hyperplane and the closest data points (support vectors) from each class. Maximizing the margin helps SVM generalize well to unseen data and improves its performance.
Support Vectors:
Support vectors are the data points that lie closest to the hyperplane and influence its position. These points are crucial in defining the decision boundary and are used to maximize the margin.
Kernel Trick:
SVM can efficiently handle non-linearly separable data by mapping the input features into a higher-dimensional space using a kernel function. The kernel function computes the dot product between feature vectors in the higher-dimensional space without explicitly transforming them. Common kernel functions include linear, polynomial, and radial basis function (RBF) kernels.
C Parameter:
SVM has a regularization parameter, often denoted as C, that controls the trade-off between maximizing the margin and minimizing the classification error. A smaller value of C allows for a wider margin but may lead to misclassification of some data points, while a larger value of C reduces the margin to classify more data points correctly.
Soft Margin SVM:
In cases where the data is not linearly separable or contains outliers, SVM uses a soft margin approach. Soft margin SVM allows for some misclassification errors by introducing slack variables, which penalize data points that fall on the wrong side of the margin or hyperplane.
Regression with SVM:
In regression tasks, SVM aims to find a hyperplane that best fits the data points while minimizing the error between the predicted and actual values. The epsilon-insensitive loss function is used to define a margin of tolerance around the fitted hyperplane.
In summary, Support Vector Machines (SVM) is a powerful algorithm for both classification and regression tasks. By finding the hyperplane that best separates different classes in the feature space, SVM achieves effective decision boundaries and generalization performance.
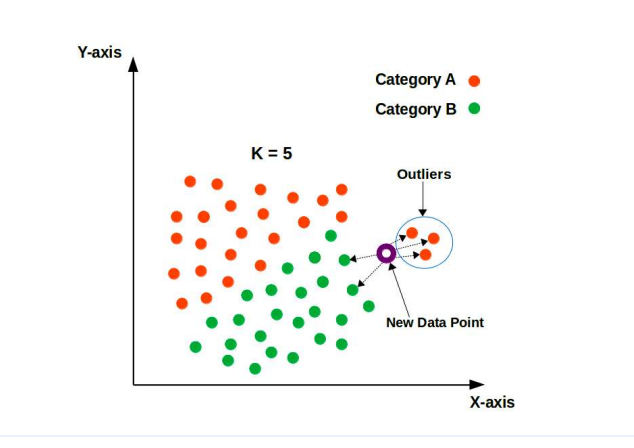
K-Nearest Neighbors (KNN)
K-Nearest Neighbors (KNN) is a straightforward yet powerful algorithm used for classification and regression tasks. Let’s explore how KNN works in simple terms:
Nearest Neighbor Classification:
In KNN, the classification of a data point is determined by the majority class among its k nearest neighbors in the feature space.
Distance Metric:
KNN calculates the distance between data points using a chosen distance metric, commonly the Euclidean distance. Other distance metrics such as Manhattan distance or cosine similarity can also be used depending on the nature of the data.
Choosing ‘k’:
The value of ‘k’ represents the number of nearest neighbors to consider when making a prediction. It is an important hyperparameter in KNN and can significantly impact the model’s performance.
Classification Decision:
Once the ‘k’ nearest neighbors are identified, KNN takes a majority vote among them to determine the class of the data point being classified. The class with the highest number of occurrences among the neighbors is assigned to the data point.
Handling Ties:
In cases where there is a tie among classes, KNN may employ various tie-breaking strategies such as selecting the class of the nearest neighbor or assigning equal weights to all neighbors.
Training Phase:
KNN is a lazy learner, meaning it does not explicitly learn a model during the training phase. Instead, it stores all training data points and their corresponding class labels in memory for later use during classification.
Testing Phase:
During the testing phase, KNN calculates the distance between the test data point and all training data points. It then identifies the ‘k’ nearest neighbors and predicts the class based on their majority vote.
Regression with KNN:
In addition to classification, KNN can also be used for regression tasks. Instead of taking a majority vote, KNN calculates the average (or weighted average) of the target values of its ‘k’ nearest neighbors to predict the continuous value for the test data point.
In summary, K-Nearest Neighbors (KNN) is a simple yet effective algorithm for classification and regression tasks. By relying on the majority class of its nearest neighbors, KNN provides an intuitive and interpretable approach to making predictions in the feature space.