6May, 2022
The Most Comprehensive NumPy Tutorial for Data Science Beginners

What is numpy ?​

NumPy is a key Python library that every data scientist should be familiar with. This thorough NumPy tutorial walks you through the basics of NumPy, from basic mathematical operations to how Numpy interacts with picture data.

Before we start the Numpy course, it’s important to note that when individuals first start working with NLP (Natural Language Processing), they utilise default Python lists

They eventually switch to Numpy, though. This is due to the fact that larger experiments with a lot of data aren’t necessarily compatible with standard Python lists. Numpy comes in handy when Python lists use too much memory.

NumPy is a Python library that stands for ‘Numerical Python’. It is a powerful library for performing mathematical and statistical operations on arrays of data. It is an essential library for scientific computing with Python.

Some of the key features of NumPy are:

  • It provides an efficient implementation of multi-dimensional arrays, which allows you to perform mathematical operations on large datasets.
  • It provides functions for performing mathematical operations on arrays, such as linear algebra operations, statistical functions, and random number generation.
  • It integrates seamlessly with other scientific libraries in Python, such as SciPy and Matplotlib, making it easy to use in scientific and data-intensive applications.
  • Overall, NumPy is an essential tool for anyone working with numerical data in Python, and is an important part of the scientific Python ecosystem.
  • NumPy is a Python library that is used for scientific computing and working with large arrays and matrices of numerical data. It provides functions for performing operations on these arrays, such as mathematical, logical, shape manipulation, sorting, selecting, I/O, discrete Fourier transforms, basic linear algebra, basic statistical operations, etc. NumPy is used extensively in data science and machine learning, and it is a fundamental package for scientific computing with Python.
  • NumPy is a Python library that is widely used for scientific and numerical computing. It provides functions and data structures for efficient computation of multi-dimensional arrays, and is designed to be integrated with other scientific libraries, such as SciPy and Matplotlib.
  • There are several reasons why NumPy is important:
  • It provides an efficient implementation of multi-dimensional arrays, which allows you to perform mathematical operations on large datasets.
  • It has functions for performing mathematical operations on arrays, such as linear algebra, statistical operations, and trigonometric functions.
  • It allows you to perform operations on arrays using vectorized operations, which can be much faster than using Python’s built-in functions or loops.
  •  
  • It integrates well with other scientific libraries in Python, such as SciPy and Matplotlib, which makes it easy to use NumPy in a scientific computing workflow.
  •  
  • Overall, NumPy is an essential library for scientific computing in Python, and is a good choice for working with large datasets and performing mathematical operations on arrays.

 

why numpy for Data analytics

NumPy is a library for Python that is designed for efficient numerical computations, particularly for working with large arrays and matrices of data. It provides a wide range of functions and operations that allow you to perform mathematical, statistical, and logical operations on large datasets efficiently. NumPy is particularly useful for data analysis because it allows you to perform complex operations on large datasets quickly and easily, without the need to write long blocks of custom code. It is also optimized for performance, so it can handle large datasets without slowing down your analysis.

NumPy is a library for the Python programming language that is commonly used in data science and scientific computing. It provides support for large, multi-dimensional arrays and matrices of numerical data, and functions to manipulate and perform operations on these with high efficiency. NumPy is particularly useful for performing mathematical and statistical operations on large datasets, and it has a number of features that make it a powerful tool for data analysis, such as its ability to perform operations on entire arrays, rather than having to loop over the elements of the array yourself.

Now you need to import the library:

Implementing Numpy in PyCharm

import numpy as np

np is the de facto abbreviation for NumPy used by the data science community.

importing NumPy
To use NumPy, you need to import it in your Python script:

import numpy as np

You can then use np as an alias for numpy. For example, you can use np.array to create a new numpy array.

a = np.array([1, 2, 3])

You can also import specific functions from the numpy library. For example:

from numpy import pi

This will import the pi constant from numpy, which can then be used as follows:

x = pi

 

NumPy Array

A Numpy Array, also known as a Numpy matrix, is a two-dimensional array with rows and columns. A NumPy array with four columns and three rows is shown below.

A NumPy array is a multidimensional array of homogeneous data (elements of the same type, such as integers or floating point values) that is used to store and manipulate large arrays of numerical data. NumPy arrays are more efficient and more convenient to use than Python’s built-in list or tuple objects, because they allow you to perform element-wise operations (operations that are applied to each element in the array) and mathematical operations with entire arrays. NumPy arrays also support more advanced indexing and slicing techniques than Python lists.

Here is an example of how to create a NumPy array:

import numpy as np

# Create a NumPy array from a Python list
array = np.array([1, 2, 3, 4, 5])
print(array)


# Output: [2 3 4 5]

 

# Create a NumPy array of zeros
zeros = np.zeros((3, 3))
print(zeros)

# Output:
# [[0. 0. 0.]
# [0. 0. 0.]
# [0. 0. 0.]]

 

# Create a NumPy array of ones
ones = np.ones((3, 3))
print(ones)

 


# Output:
# [[1. 1. 1.]
# [1. 1. 1.]
# [1. 1. 1.]]

 

# Create a NumPy array with random values
random = np.random.random((3, 3))
print(random)

 


# Output:
# [[0.44444444 0.66666667 0.66666667]
# [0.22222222 0.44444444 0.88888889]
# [0.55555556 0.22222222 0.44444444]]

You can also specify the data type of the elements in the array when you create it, using the dtype parameter:

# Create a NumPy array with integers
array = np.array([1, 2, 3, 4, 5], dtype=np.int32)
print(array)

 


# Output: [1 2 3 4 5]

 

# Create a NumPy array with floating point values
array = np.array([1.1, 2.2, 3.3, 4.4, 5.5], dtype=np.float64)
print(array)

 


# Output: [1.1 2.2 3.3 4.4 5.5]

You can access elements in a NumPy array using indexing, just like you would with a Python list:

import numpy as np
array = np.array([1, 2, 3, 4, 5])

# Get the first element
print(array[0]) #

 

Output: 1

# Get the last element
print(array[-1]) # Output: 5

# Get the second to last element
print(array[-2]) # Output: 4

# Get the first three elements
print(array[:3]) # Output: [1 2 3]

# Get the last three elements
print(array[-3:]) # Output: [3 4 5]

NumPy Arrays vs. Python Lists — What Is the Distinction?

If you know Python, you might be questioning why we need NumPy arrays since we already have Python lists. After all, these Python lists function as an array that may store numerous sorts of items. This is an excellent question, and the solution lies in the way Python keeps objects in memory.

A Python object is essentially a reference to a memory region that contains all of the object’s characteristics, such as bytes and value. Although this extra information is what makes Python a dynamically typed language, it comes at a cost, which is evident when keeping a big collection of objects, such as in an array.

Python lists are just an array of pointers, each referring to a different item in the list.

Python lists are basically an array of pointers, each pointing to a location containing the element’s information. 
This adds a significant amount of memory and calculation overhead. 
When all of the items in the list are of the same type, most of this information is rendered irrelevant!
To get around this, we utilise NumPy arrays with only main emphasis, that is, items of the same data type. 
This improves the array’s storage and manipulation efficiency. 
When the array has a big number of elements, such as hundreds or millions, this difference becomes obvious. 
You can also execute element-wise operations with NumPy arrays, which is not feasible with Python lists!

Python, a list is a collection of values that can be of any data type, including other lists. Lists are dynamic, which means you can add or remove elements from a list after it is created. They are also indexed, which means you can access the elements of a list by their position in the list.

NumPy arrays are similar to lists, but they are fixed in size and each element has the same data type. NumPy arrays are more efficient for certain operations because they allow you to perform element-wise operations on the entire array, rather than having to loop over the elements of the list yourself. NumPy arrays are also more memory efficient than lists, because they store the data in a contiguous block of memory.

Here is an example to illustrate the differences between lists and NumPy arrays:

import numpy as np

array = np.array([1, 2, 3, 4, 5])

# Get the first element
print(array[0]) # Output: 1

# Get the last element
print(array[-1]) # Output: 5

# Get the second to last element
print(array[-2]) # Output: 4

# Get the first three elements
print(array[:3]) # Output: [1 2 3]

# Get the last three elements
print(array[-3:]) # Output: [3 4 5]

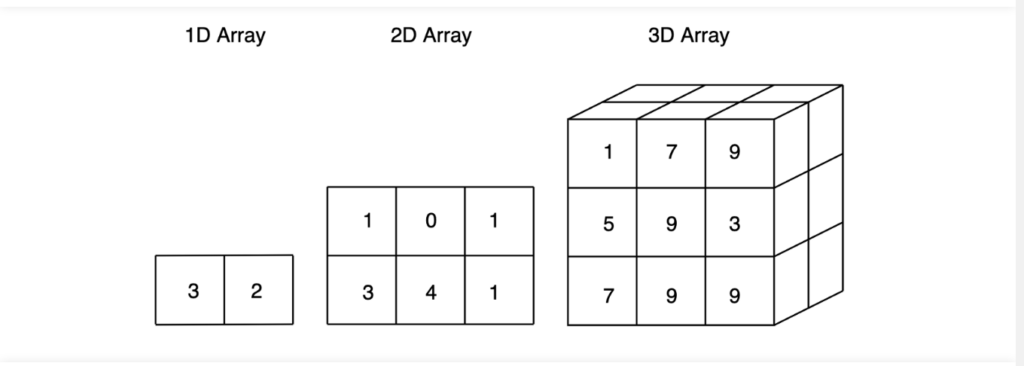
numpy array

1d 2d 3d array in numpy pyhton

NumPy is a powerful library for working with multi-dimensional arrays in Python. You can create a 1D array, 2D array, or 3D array using the numpy library as follows:

To create a 1D array:

import numpy as np

# create a 1D array with 10 elements
array_1d = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
print(array_1d)

Output: [0 1 2 3 4 5 6 7 8 9]

To create a 2D array:

import numpy as np

# create a 2D array with 3 rows and 4 columns
array_2d = np.array([[0, 1, 2, 3], [4, 5, 6, 7], [8, 9, 10, 11]])
print(array_2d)

Output:

[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]

To create a 3D array:

import numpy as np

# create a 3D array with 2x3x4 array
array_3d = np.array([[[0, 1, 2, 3], [4, 5, 6, 7], [8, 9, 10, 11]], 
[[12, 13, 14, 15], [16, 17, 18, 19], [20, 21, 22, 23]]])
print(array_3d)

Output:

[[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]

[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]]

Indexing and slicing

To index an array in Python, you can use the square brackets [] with the index number inside. Array indexes start at 0, so the first element of an array is at index 0. For example:

arr = [1, 2, 3, 4, 5]
print(arr[0]) # Output: 1
print(arr[2]) # Output: 3
print(arr[4]) # Output: 5

ou can also use negative indexes to access elements from the end of the array. For example:

print(arr[-1]) # Output: 5
print(arr[-2]) # Output: 4
print(arr[-5]) # Output: 1

How do you know the shape and size of an array?

In most programming languages, you can determine the shape and size of an array by using built-in functions or methods.

For example, in Python, you can use the shape attribute of a NumPy array to get its dimensions, and the size attribute to get the total number of elements in the array.

Here’s an example:

import numpy as np

# Create a 2x3 array
arr = np.array([[1, 2, 3], [4, 5, 6]])
# Get the shape and size of the array
shape = arr.shape
size = arr.size

print(f"Shape: {shape}")
print(f"Size: {size}")

NumPy matrix in the same shape but as a different array

(i) Numpy Tutorial: How to create a NumPy matrix in the same shape but as a different array. This uses the function NumPy.empty_like():

# Creating ndarray from list
c = np.array([[1., 2.,],[1., 2.]])
# Creating new array in the shape of c, filled with 0
d = np.empty_like(c)

(ii) Then you cast the NumPy array from the Python list using the function NumPy.asarray() :

import NumPy as np

list = [1, 2, 3]
c = np.asarray(list)

(iii) You can also create a customized ndarray in the required size. You can fill it with random values, ones, or zeroes.

# Array items as ndarray
c = np.array([1, 2, 3])

# A 2×2 2d array shape for the arrays in the format (rows, columns)
shape = (2, 2)

# Random values
c = np.empty(shape)
d = np.ones(shape)
e = np.zeros(shape)

Can you reshape an array?

Yes, it is possible to reshape an array in a variety of programming languages. In many languages, you can use the reshape function to change the number of rows and columns in an array and rearrange its elements. For example, in Python, you can use the numpy library to reshape an array like this:

import numpy as np

# Create a 2×3 array
arr = np.array([[1, 2, 3], [4, 5, 6]])

# Get the shape and size of the array
shape = arr.shape
size = arr.size

print(f"Shape: {shape}")
print(f"Size: {size}")

This will output the following:

Shape: (2, 3)
Size: 6

10 functions in NumPy that are most commonly used: with example

1. array: creates an array from a list or tuple. For example:

import numpy as np

arr = np.array([1, 2, 3])
print(arr) # prints [1 2 3]

2.zeros: creates an array of a specified size filled with zeros. For example:

import numpy as np

arr = np.zeros(5)
print(arr) # prints [0. 0. 0. 0. 0.]

3.ones: creates an array of a specified size filled with ones. For example:

import numpy as np

arr = np.ones((3, 3))
print(arr) # prints [[1. 1. 1.], [1. 1. 1.], [1. 1. 1.]]

4.arange: creates an array with evenly spaced values within a given range. For example:

import numpy as np

arr = np.arange(0, 10, 2)
print(arr) # prints [0 2 4 6 8]

5.linspace: creates an array with a specified number of equally spaced values between two endpoints. For example:

import numpy as np

arr = np.linspace(0, 10, 5)
print(arr) # prints [ 0. 2.5 5. 7.5 10. ]

6.reshape: reshapes an array to a specified size. For example:

import numpy as np

arr = np.array([1, 2, 3, 4, 5, 6])
arr = arr.reshape((2, 3))
print(arr) # prints [[1 2 3], [4 5 6]]

7.max: returns the maximum value in an array. For example:

import numpy as np

arr = np.array([1, 5, 2, 7, 3])
max_val = np.max(arr)
print(max_val) # prints 7

8.min: returns the minimum value in an array. For example:

import numpy as np

arr = np.array([1, 5, 2, 7, 3])
min_val = np.min(arr)
print(min_val) # prints 1

9.argmax: returns the index of the maximum value in an array. For example:

import numpy as np

arr = np.array([1, 5, 2, 7, 3])
max_index = np.argmax(arr)
print(max_index) # prints 3

How to Merge Arrays with Numpy Python

Rather than merging arrays, you should build an array of the desired size and fill it. This is due to the fact that merging arrays only results in the construction of a large array and the copying of the contents into it.

Use these routines instead if you need to combine arrays.

Concatenate

1d arrays:

a = np.array([1, 2, 3])
b = np.array([5, 6])
print np.concatenate([a, b, b])

# >> [1 2 3 5 6 5 6]

2d arrays:

a2 = np.array([[1, 2], [3, 4]])
# axis=0 – concatenate along rows
print np.concatenate((a2, b), axis=0)
# >> [[1 2]
# [3 4]
# [5 6]]
# axis=1 – concatenate along columns, but first b needs to be transposed:
b.T
#>> [[5]
# [6]]
np.concatenate((a2, b.T), axis=1)
#>> [[1 2 5]
# [3 4 6]]

Append

1d arrays:

# 1d arrays
print np.append(a, a2)
# >> [1 2 3 1 2 3 4]

print np.append(a, a)
# >> [1 2 3 1 2 3]

2d arrays.

append(a2, b, axis=0)
# >> [[1 2]
# [3 4]
# [5 6]]

print np.append(a2, b.T, axis=1)
# >> [[1 2 5]
# [3 4 6]]

Python NumPy Operations

ndim: 


You can determine the array’s dimension, whether it’s a two-dimensional or single-dimensional array. So, let’s look at how we may find the dimensions in practise. I can determine whether the array is single or multidimensional using the ndim function in the code below.

1

import numpy as np

2

a = np.array([(1,2,3),(4,5,6)])

3

print(a.ndim)

Output – 2
It’s a two-dimension array because the output is 2. (multi dimension).

 

itemsize:

Each element’s byte size can be calculated. I’ve defined a single-dimensional array in the code below, and we can discover the size of each element using the ‘itemsize’ function.

1

import numpy as np

2

a = np.array([(1,2,3)])

3

print(a.itemsize)

Output – 4

In the numpy array above, each element takes up 4 bytes.

 

Hstack (stack horizontally) and vstack (stack vertically)

1d arrays:

print np.hstack([a, b])
# >> [1 2 3 5 6]

print np.vstack([a, a])
# >> [[1 2 3]
# [1 2 3]]

2d arrays:

print np.hstack([a2,a2]) # arrays must match shape
# >> [[1 2 1 2]
# [3 4 3 4]]
print np.vstack([a2, b])
# >> [[1 2]
# [3 4]
# [5 6]]

linspace

Linspace delivers numbers that are evenly spaced throughout a given interval. For example:

1

import numpy as np

2

a=np.linspace(1,3,10)

3

print(a)

Output – [ 1. 1.22222222 1.44444444 1.66666667 1.88888889 2.11111111 2.33333333 2.55555556 2.77777778 3

Square Root and Standard Deviation in Numpy

The square root function returns the square root of each and every output element. You may also get the standard deviation. Let’s see what happens.

1

import numpy as np

2

a=np.array([(1,2,3),(3,4,5,)])

3

print(np.sqrt(a))

4

print(np.std(a))


Max/Min Numpy Tutorial


This function is useful for determining the minimum and maximum values of a NumPy array.

1

import numpy as np

2

a= np.array([1,2,3])

3

print(a.min())

4

print(a.max())

5

print(a.sum())

 

Numpy Tutorial: Python Numpy Special Functions

Mathematical functions like sine, tan, cos, log, etc can also be used you can use in NumPy. We can plot the sine, cos, tan function by importing Matplotlib. Here’s what it looks like for the sine function:

1

import numpy as np

2

import matplotlib.pyplot as plt

3

x= np.arange(0,3*np.pi,0.1)

4

y=np.sin(x)

5

plt.plot(x,y)

6

plt.show()

 

Final thought

NumPy is an excellent tool for emerging data scientists who want to execute more complex operations with big volumes of data than the basic Python lists.

There are many more operations that may be performed with these Python Tools that are not covered in this Numpy lesson. You can progress to more sophisticated operations once you’ve mastered the NumPy basics.

 

Are the possibilities presented by Python inspiring you as well? You can also enrol in a Data Science Course for more profitable career opportunities in Python Data Science.

DATA SCIENCE TRAINING

NumPy is a Python library that stands for ‘Numerical Python’. It is a powerful library for performing mathematical and statistical operations on arrays of data. It is an essential library for scientific computing with Python.

Some of the key features of NumPy are:

  • It provides an efficient implementation of multi-dimensional arrays, which allows you to perform mathematical operations on large datasets.
  • It provides functions for performing mathematical operations on arrays, such as linear algebra operations, statistical functions, and random number generation.
  • It integrates seamlessly with other scientific libraries in Python, such as SciPy and Matplotlib, making it easy to use in scientific and data-intensive applications.
  • Overall, NumPy is an essential tool for anyone working with numerical data in Python, and is an important part of the scientific Python ecosystem.
  • NumPy is a Python library that is used for scientific computing and working with large arrays and matrices of numerical data. It provides functions for performing operations on these arrays, such as mathematical, logical, shape manipulation, sorting, selecting, I/O, discrete Fourier transforms, basic linear algebra, basic statistical operations, etc. NumPy is used extensively in data science and machine learning, and it is a fundamental package for scientific computing with Python.
  • NumPy is a Python library that is widely used for scientific and numerical computing. It provides functions and data structures for efficient computation of multi-dimensional arrays, and is designed to be integrated with other scientific libraries, such as SciPy and Matplotlib.
  • There are several reasons why NumPy is important:
  • It provides an efficient implementation of multi-dimensional arrays, which allows you to perform mathematical operations on large datasets.
  • It has functions for performing mathematical operations on arrays, such as linear algebra, statistical operations, and trigonometric functions.
  • It allows you to perform operations on arrays using vectorized operations, which can be much faster than using Python’s built-in functions or loops.
  •  
  • It integrates well with other scientific libraries in Python, such as SciPy and Matplotlib, which makes it easy to use NumPy in a scientific computing workflow.
  •  
  • Overall, NumPy is an essential library for scientific computing in Python, and is a good choice for working with large datasets and performing mathematical operations on arrays.

 

Data Cleaning With pandas and NumPy in Python